Question

A 1.5 kg box moves back and forth on a horizontal frictionless surface between two different springs as shown in the figure the box is initially pressed against the stronger spring compressing it 4 cm and then is released from rest bye how much will the box compress the weaker spring

Answer 1

Given,

The mass of the box, 1.5 kg

The spring constant of the stronger spring, k₁=32 N/cm

The spring constant of the weaker spring, k₂=16 N/cm

The compression of the stronger spring, x₁=4 cm

When the spring is compressed, there will be certain potential energy stored in the spring. While expanding, the spring loses the potential energy. In this case, the potential energy lost by the stronger spring will be gained by the box in the form of kinetic energy, according to the law of conservation of energy.

With this kinetic energy, the box will have velocity. The box will move across the surface without losing its kinetic energy as the surface is frictionless. And then the box presses against the weaker spring and compresses it. While compressing the spring, the box transfers all its kinetic energy to the spring.

Thus the potential energy lost by the stronger spring is equal to the potential energy gained by the weaker spring.

Thus,

`\frac{1}{2\text{ }}k_1x^2_1=(1)/(2)k_2x^2_2`

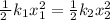
Where x₂ is the compression of the weaker spring.

On rearranging the above equation,

`x_2=\sqrt[]{(k_1x^2_1)/(k_2)}`

On substituting the known values,

`\begin{gathered} x_2=\sqrt[]{(32*4^2)/(16)} \\ =5.66\text{ cm} \end{gathered}`

Thus the box will compress the spring by 5.66 cm