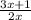Question

help me answer this. Complex Fractions: Identify the steps used in simplifying the following complex fraction:

Answer 1

We need to simplify the following expression:

`((1)/(2(x+1))+(1)/(x-1))/((1)/(x^(2)-1)+(1)/(x+1))`

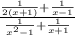
We can start by finding the LCD (least common denominator) for the numerator and for the denominator of the expression.

First, let's find the LCD of the numerator.

Since the denominators of the fractions:

`(1)/(2(x+1))\text{ and }(1)/(x-1)`

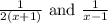
have no common factors, the LCD of those expressions is:

`2(x+1)(x-1)=2(x^(2)-1)`

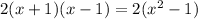
Thus, we can simplify the numerator as:

`(x-1+2x+2)/(2(x^(2)-1))=(3x+1)/(2(x^(2)-1))`

Now, we can find the LCD of the denominator.

Since x²-1 is a multiple of x+1, the LCD is:

`x^(2)-1`

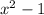
Thus, we can simplify the denominator as:

`(1+x-1)/(x^(2)-1)=(x)/(x^(2)-1)`

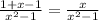
Then, we obtained the equivalent expression:

`((3x+1)/(2(x^2-1)))/((x)/(x^2-1))`

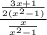
Now, we need to find the reciprocal of the denominator, to write the division as a product:

`\text{reciprocal of }(x)/(x^(2)-1)=(x^(2)-1)/(x)`

Thus, we obtain:

`((3x+1)/(2(x^2-1)))/((x)/(x^2-1))=(3x+1)/(2(x^2-1))\cdot(x^(2)-1)/(x)`

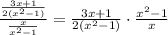
Then, we simplify the complex fraction:

`(3x+1)/(2(x^2-1))\cdot(x^2-1)/(x)=(3x+1)/(2x)`

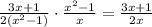
Therefore, after simplifying, we obtain:

`(3x+1)/(2x)`