Question

A 5th-degree polynomial has three of its roots, 1, 2i, and i. Find the polynomial in factored form

Answer 1

Given the roots,

`1,2i,i`

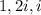
To have a polynomial with real coefficients, the complex conjugates of 2i and i must be roots of the polynomial as well

The conjugate of 2i is -2i while the conjugate of i is -i

The roots of the polynomial will be

`1,2i,-2i,i,-i`

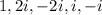
The factors of the polynomial will be

`(x-1),(x-2i),(x+2i),(x-i),(x+i)`

The factored form of the polynomial will be

`\begin{gathered} f(x)=(x-1)(x-2i)(x+2i)(x-i)(x+i) \\ f(x)=(x^2+1)(x^2+4)(x-1) \end{gathered}`

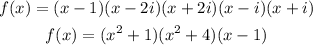
Hence, answer is option A