Between 77 and 129
Here, we want to describe where the lowest 5% and the highest 5% of IQ scores lie
What we need here is the appropriate z-score that corresponds to both the lowest 5% and the highest 5%
For the lowest 5%, we have a z-score of -1.645 while for the highest 5% (95% - 100%), we have a z-score of 1.645
Mathematically, the formula for calculating the z-score for a normal distribution is as follows;
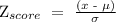
Where σ is the standard deviation = 13 and μ = 103 which is the mean. X refer to the raw IQ scores which we are trying to calculate
Thus;
for z = -1.645
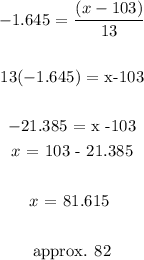
For z = 1.645

So we have the range of between 82 and 124
We now proceed to the options to check the best fit
The best fit here is between 77 and 129