Reflection of (x,y ) over y=-x is (-y, -x)
That is;
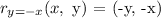
A(4, 8) ⇒ A'(-8, -4)
B(6, 8) ⇒ B' (-8, -6)
C(8, 5) ⇒ C' (-5, -8)
D(2, 5) ⇒ D' (-5, -2)
Rotation of (x, y) clockwise about the origin over 90 degrees is (y, -x)
That is;
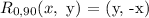
A' (-8, -4) ⇒ A"( -4, 8)
B'(-8, -6) ⇒ B" (-6, 8)
C' (-5, -8) ⇒ C" (-8 , 5)
D' (-5, -2) ⇒ D" (-2, 5)
Part B
Reflection of the polygon A''B'' C'' D'' over y will carry the polygon to ABCD