Question

5. Match each equation with the slope m and y-intercept of its graph.5x - 6y = 30 y = 5-6x y = 5/6x +1 5x - by = 6 5x + 6y = 6 6x + y = 12m=-6. y-int= (0,12)m=-6. y-int= (0,5)m = -5/6,int = (0,1)m = 5/6,int = (0,1)Oom = 5/6.int = (0-1)om = 5/6, yint = (0,-5)

Answer 1

Hello!

First, we have to remember that the equation of the line has the form:

y = mx + b

• m, = slope

,

• b, = y-intersection

Knowing it, we can solve this exercise:

1st equation: 5x -6y = 30

Let's isolate y:

`\begin{gathered} 5x-6y=30 \\ -6y=30-5x \\ -y=(30)/(6)-(5x)/(6) \\ (-1)\cdot-y=5-(5x)/(6)\cdot(-1) \\ y=(5x)/(6)-5 \end{gathered}`

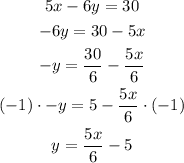
Slope: 5/6

Y-intercept: (0, -5)

2nd equation: y = 5 -6x

Slope: -6x

Y-intercept: (0, 5)

3rd equation: y = 5/6x +1

Slope: 5/6

Y-intercept: (0, 1)

4th equation: 5x -6y = 6

Let's isolate y:

`\begin{gathered} 5x-6y=6 \\ -6y=6-5x \\ -y=(6)/(6)-(5x)/(6) \\ (-1)\cdot-y=1-(5x)/(6)\cdot(-1) \\ y=(5x)/(6)-1 \end{gathered}`

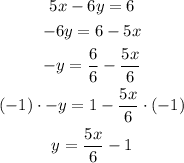
Slope: 5/6

Y-intercept: (0, -1)

5th equation: 5x + 6y = 6

Let's isolate y:

`\begin{gathered} 5x+6y=6 \\ 6y=6-5x \\ y=(6)/(6)-(5x)/(6) \\ y=-(5x)/(6)+1 \end{gathered}`

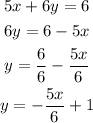
Slope: -5/6

Y-intercept: (0, 1)

6th equation: 6x +y = 12

`y=-6x+12`

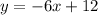
Slope: -6

Y-intercept: (0, 12)

Look at your answers below: