hello
from the image given, we have two right angle triangle diagonally infused together. we have two equal lines that connects the two triangles
we can use trigonometric ratios and imploy sine of the angle to solve for this problem since we have the value of hypothenus and angle
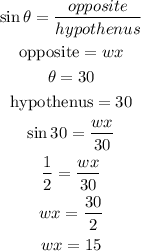
from the calculation above, the value of wx is equal to 15 units