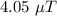Given:
The distance between the wires is,
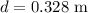
The currents in each wire are in the same direction and the magnitude is,
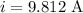
To find:
The net magnetic field 0.832 m away from each wire on the side opposite the other wire
Step-by-step explanation:
The magnetic field due to a current-carrying wire is,
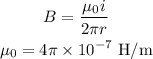
If we see the diagram of both the wires,
the point x is at a distance (x+d) from the second wire
The magnetic field due to wire 1 and wire 2 will be out of the page.
The net magnetic field at point x is,
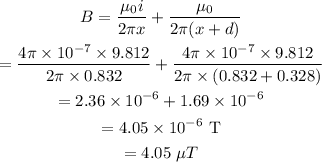
Similarly, on the right of wire 2, the magnetic field will be the same but into the page.
Hence, the required magnetic field is,