Question

Graph the parabola.Y=x^2+4Plot five points on the parabola: The vertex, two points to the left of the vertex, and two points to the right of the vertex.

Answer 1

Notice that the equation of the given parabola is in vertex form, therefore the vertex of the given parabola is:

`(0,4).`

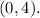
Recall that to evaluate an equation at a given value we substitute the variable with the given value.

Evaluating the given equation at x=-2 we get:

`y=(-2)^2+4=4+4=8.`

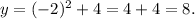
Therefore the graph of the given parabola passes through (-2,8).

Evaluating the given equation at x=-1 we get:

`y=(-1)^2+4=1+4=5.`

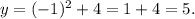
Therefore the graph of the given parabola passes through (-1,5).

Evaluating the given equation at x=2 we get:

`y=2^2+4=4+4=8.`

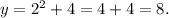
Therefore the graph of the given parabola passes through (2,8).

Evaluating the given equation at x=1 we get:

`y=1^2+4=1+4=5.`

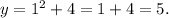
Therefore the graph of the given parabola passes through (1,5).

Therefore the graph of the given parabola is:

Answer:

The vertex is (0,4).

Two points to the left of the vertex are (-2,8) and (-1,5).

Two points to the right of the vertex are (2,8) and (1,5).