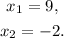We must solve for x the following equation: "zero equals X squared minus 7X -18", mathematically this equation is:

Solving this equation is equivalent to find the roots of a polynomial of degree 2. A polynomial of degree 2 always has 2 roots, and they are given by the following equations:
![\begin{gathered} x_1=\frac{-b+\sqrt[]{b^2-4ac}}{2a}, \\ x_2=\frac{-b-\sqrt[]{b^2-4ac}}{2a}, \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/moh742sly07r2g1eumg7k38ffrgxlntbwg.png)
where the coefficients a, b and c are coefficients of each term of the polynomial:
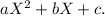
Comparing with the polynomial of the problem, we see that the coefficients are:
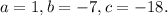
Replacing the values of the coefficients in the formulas for the roots above, and computing, we get:
![\begin{gathered} x_1=\frac{-(-7)+\sqrt[]{(-7)^2-4\cdot1\cdot(-18)}}{2\cdot1}=9, \\ x_2=\frac{-(-7)-\sqrt[]{(-7)^2-4\cdot1\cdot(-18)}}{2\cdot1}=-2, \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/gnxb2aho0q9wwnhp5qyhthjnyk75x9wegv.png)
Answer
The solutions to the equation of the problem are: