From the acceleration yo can find the rest of the expressions by integrating the initial equations
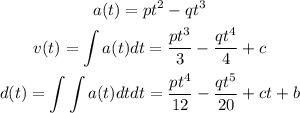
Is important to put the constants when you integrate, they can affect the result when you solve the system
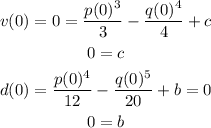
After having the expressions, you replace the assumptions, in this case, v and d are 0, when time t is 0