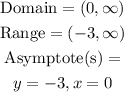Question

I’ll put what i need answered in the comments. someone please help:(

Answer 1

The graph of the function

`y=-\log _3x`

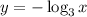
is shown below:

The domain is the set of allowed x values of the function.

The range is the set of allowed y values of the function.

If you look at the graph, the domain is x greater than 0 towards infinity. We can write it as:

`DOMAIN=(0,\infty)`

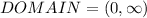
Then, take a look at this other version of the graph, zoomed in:

From this, we can clearly see that the range is y greater than -3 towards infinity. Thus, the range can be written as:

`\text{RANGE}=(-3,\infty)`

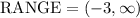
An asymptote is a line the graph gets closer and closer to but never touches it.

If we look at the graph, we see that the y-axis (x = 0 ) is an asymptote and the line y = -3 is another asymptote, so,

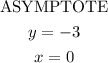
`\begin{gathered} \text{ASYMPTOTE} \\ y=-3 \\ x=0 \end{gathered}`Answers
`\begin{gathered} \text{Domain}=(0,\infty) \\ \text{Range}=(-3,\infty) \\ \text{Asymptote(s)}= \\ y=-3,x=0 \end{gathered}`