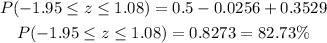Question

A local bank has determined that the daily balances of the checking accounts of its customers are normally distributed with an average of $280 and a standard deviation of $20.a.What percentage of its customers has daily balances of more than $275?b.What percentage of its customers has daily balances of less than $243?c.What percentage of its customers' balances is between $241 and $301.60?

Answer 1

a. Z-score formula

`z=(x-\mu)/(\sigma)`

where,

• x: observed value

,

• μ: mean

,

• σ: standard deviation

Substituting with x = $275, μ = $280, and σ = $20, we get:

`\begin{gathered} z=(275-280)/(20) \\ z=-0.25 \end{gathered}`

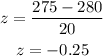
In terms of the z-score, we need to find

`P(z\ge-0.25)=1-P(z\le-0.25)`

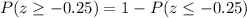
From the table:

`P(z\le-0.25)=0.4013`

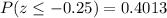
Then, the percentage of customers that has daily balances of more than $275 is:

`\begin{gathered} P(z\ge-0.25)=1-0.4013 \\ P(z\ge-0.25)\approx0.6=60\% \end{gathered}`

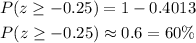
b. Substituting with x = $243, μ = $280, and σ = $20 into the z-score formula, we get:

`\begin{gathered} z=(243-280)/(20) \\ z=-1.85 \end{gathered}`

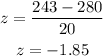
In terms of the z-score, we need to find:

`P(z\le-1.85)`

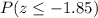
From the table, the percentage of customers that has daily balances of less than $243 is:

`P(z\le-1.85)=0.0322=3.22\%`

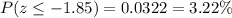
c. Substituting with x₁ = $241 and x₂ = $301.60, μ = $280, and σ = $20 into the z-score formula, we get:

`\begin{gathered} z_1=(241-280)/(20)=-1.95 \\ z_2=(301.60-280)/(20)=1.08 \end{gathered}`

In terms of the z-score, we need to find:

`\begin{gathered} P(-1.95\le z\le1.08)=P(-1.95\le z\le0)+P(0\le z\le1.08) \\ P(-1.95\le z\le1.08)=0.5-P(z\le-1.95)+P(0\le z\le1.08) \end{gathered}`

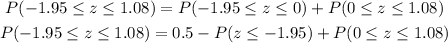
From the first table:

`P(z\le-1.95)=0.0256`

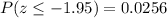
From the second table:

`P(0\le z\le1.08)=0.3529`

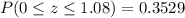
Therefore, the percentage of its customers' balances between $241 and $301.60 is:

`\begin{gathered} P(-1.95\le z\le1.08)=0.5-0.0256+0.3529 \\ P(-1.95\le z\le1.08)=0.8273=82.73\% \end{gathered}`