Question

Assume that men have weights that are normally distributed with a mean of 172 pounds and a standard deviation of 30 pounds.a) Find the probability that a randomly selected man weighs over 200 pounds.b) Find the probability that 30 randomly selected men have an average weight over 200 pounds (Use the Central Limit Theorem).c) Interpret the results.

Answer 1

The Central Limit Theorem tells us that for a population with any distribution, the distribution of the

sample means approaches a normal distribution as the sample size increases. The procedure in this

section forms the foundation for estimating population parameters and hypothesis testing.

From the given data we have,

Mean = 172 pounds

Standard Deviation = 30 pounds

Probability through the normal distribution is expresses as :

`\begin{gathered} z=(x-\mu)/(\sigma) \\ \text{ where }\mu=\text{ mean \& }\sigma=\text{ Stanadard Deviation} \end{gathered}`

a)

Probability for weighs over 200 pounds

x = 200

`\begin{gathered} z=(200-172)/(30) \\ z=0.933 \end{gathered}`

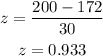
b) The probability that 30 randomly selected men have an average weight over 200 pounds is expresses as :

`\begin{gathered} z=(x-\mu)/((\sigma)/(n)) \\ \text{ where }\mu=\text{ mean, n = number \& }\sigma=\text{ Stanadard Deviation} \end{gathered}`

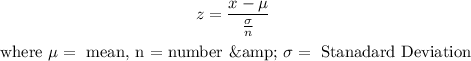
So, here n =30

`\begin{gathered} z=\frac{200-172}{\frac{30}{\sqrt[]{30}}} \\ z=(28)/(5.477) \\ z=5.11 \end{gathered}`

Answer : z=5.11