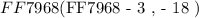Question

What is the image of (-1, -6) after a dilation by a scale factor of 3 centeredat the origin?

Answer 1

We are to investigate the effects of dilation transformation on a pair of coordinates.

The effect of dilation is merely classified by the distance of each point either served induvidual or in form of a figure to be either shortened or enlarged relative to a reference point.

The reference point of dilation can be any point on the cartesian coordinate system. The reference of dilation given to us in this problem is the origin:

`\text{Origin ( 0 , 0 )}`

The point is plotted on the cartesian coordinate system on which the transformation is to be applied:

`(\text{ - 1 , -6 )}`

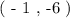
The general rule of dilation transformation with respect to the origin is expressed as follows:

`(\text{ x , y ) -> ( a}\cdot x\text{ , a}\cdot y\text{ )}`

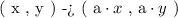
Where,

`a\colon\text{ scale factor}`

The scale factor gives us the magnitude of how large or how small the dilation is to be performed. It is generally categorized as follows:

`\begin{gathered} 0\text{ < a < 1 }\ldots\text{ Shrinking} \\ a\text{ > 1 }\ldots\text{ Enlarging} \end{gathered}`

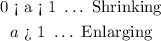
Where,

`\begin{gathered} \text{Shrinking: Reducing the distance of the point from the origin} \\ \text{Enlarging: Increasing the distance of the point from the origin} \end{gathered}`

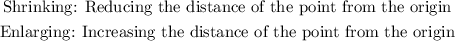
We are given the scale factor for the dilation as follows:

`\text{Scale factor ( a ) = 3}`

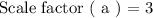
Using the abve guidelines for the scale factor ( a ). We see it is categorized as an enlarging scale! This means we will have to increase the distance of point ( -1 , -6 ) from the origin by a scale of ( a = 3 ).

We will apply the dilation rule expressed above as follows:

`\begin{gathered} (\text{ -1 , - 6 ) }\to\text{ (3}\cdot(-1)\text{ , 3}\cdot(-6\text{ ) )} \\ (\text{ -1 , - 6 ) }\to\text{ (-3 , -18 )} \end{gathered}`

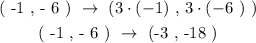
Hence the image of the point ( -1 , -6 ) after a dilation of scale factor ( 3 ) is as follows:

`\textcolor{#FF7968}{(}\text{\textcolor{#FF7968}{ - 3 , - 18 )}}`