Question

Determine whether the following points satisfy y=2x+3, y>2x+3 or y<2x-3 without drawing a grapha) (0,1)

Answer 1

The expressions are given as,

`\begin{gathered} y=2x+3 \\ y>2x+3 \\ y<2x-3 \end{gathered}`

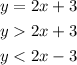
It is asked to check whether the point (0,1) satisfy all the above relationships.

Substitute the coordinate in the first equation,

`\begin{gathered} 1=2(0)+3 \\ 1=0+3 \\ 1=3 \end{gathered}`

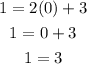
Clearly, the result is not true. So it can be concluded that the point (0,1) does not satisfy the first relationship.

Substitute the coordinate in the second inequation,

`\begin{gathered} 1>2(0)+3 \\ 1>0+3 \\ 1>3 \end{gathered}`

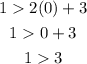
Again, the result is not true. So it can be concluded that the point (0,1) does not satisfy the second relationship.

Substitute the coordinate in the third inequation,

`\begin{gathered} 1<2(0)-3 \\ 1<0-3 \\ 1<-3 \end{gathered}`

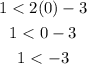
This result obtained is true. So it can be concluded that the point (0,1) satisfies the third relationship.

Thus, the given point satisfies the third relationship only.