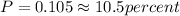We need to find the probability that two people are selected from the accounting department and one will be from the sales department. To do that, we need first to determine the total amount of people. We have that for each department the number of people is:
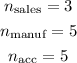
Therefore, the total number of people is:
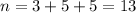
Now, for this problem, we need to use combinatoric of a selection without replacement. The number of possible combinations of possible "r" combinations of a population of "n" individuals is given by the formula:
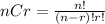
In our case we have to determine first the total number of combinations from selecting 3 people of the total population, that is:
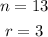
replacing in the formula we get:
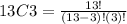
Solving the operations we get:
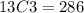
Now we find the possible combination of getting 2 people from a total of 5 people from the accounting department, that is:
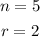
replacing in the formula we get:
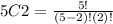
Solving the operations we get:
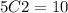
Now we find the total combinations of getting 1 person from a total of 3 people in the sales department, that is:
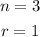
Replacing in the formula:
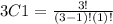
Solving the operations we get:
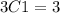
The total number of possible outcomes is then the product of both combinations, that is:
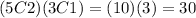
The probability is then given by the formula:
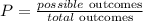
Replacing we get:
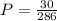
Solving we get: