Question

Use the line plot to answerthe questions below.XХХХXXXХХхХXXXXX ХХХ8. How many numbers aregreater than 28?ft24 25 2629 30 319. Find the mean, median, mode, and range of the data from the line plot belowX+27+32283334

Answer 1

hello

to find the total numbers that are greater than 28, we'll count the numbers of asterix on numbers greater than 28

`\begin{gathered} \text{numbers asterix} \\ 29\text{ ====== 3} \\ 30\text{ ====== 3} \\ 31\text{ ====== 3} \\ 32\text{ ====== 0} \\ 33\text{ ====== 1} \\ 34\text{ ====== 1} \\ \text{total numbers greater than 28 = 3 + 3 + 3 + 1 + 1 = 11} \end{gathered}`

2. The Mean, Median, and Range of the data

the range of any data is the difference between the heighest and lowest value

`\begin{gathered} \text{heighest value = }34 \\ \text{lowest value = }25 \\ \text{range = heighest value - lowest value} \\ \text{range = 34 - 25 } \\ \text{range = 9} \end{gathered}`

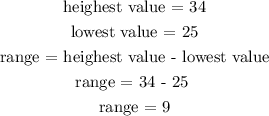
mode

The mode of any data set is the heighest occuring number in a given date set

in this question, the mode would be between 26 and 28 and this data set can be said to bimodal.

Median

Median is the middle number in a given data set that is arranged from the least to the heighest.

in this case, the median can be calculated as

Mean

The mean of any given data set is the average of the data. This can be calculated by finding the total sum of the data and divide by the total number of addens