Given:
The time duration of the operation of the laser is t = 19.76 s
The power of the laser is P = 4.54 W
The wavelength of the red laser is
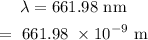
Required: The number of photons.
Step-by-step explanation:
In order to calculate the number of photons, first, we need to calculate the total energy of the photons.
The total energy of the photons can be calculated as
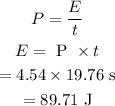
The energy of one photon is given by the formula
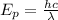
Here, h is the Planck's constant whose value is
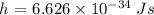
c is the speed of light whose value is
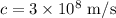
On substituting the values, the energy of one photon will be
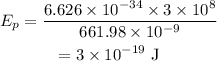
The number of photons can be calculated as
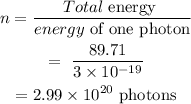
Final Answer: There are 2.99e20 photons during the operation of the red laser pointer.