The data set given are: 30, 30, 42, 18, 42, 24
The formula for the mean of the data set is:

The formula for standard deviation (S.D) is:
![\begin{gathered} S.D\text{ = }\sqrt[]{\frac{\Sigma|x-\bar{x}|^2}{n}} \\ \text{ where, }\bar{x}=\text{ mean, n= number of data} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/urlhubnm7t8h0mezdudg147znj6z30axd7.png)
Step 1: Find the mean
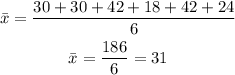
step 2: Find the summation of the absolute value deviation of the data from the mean
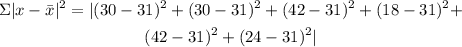
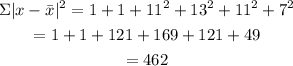
step 3: Substitute the value obtained in step 2 into the standard deviation formula
![\begin{gathered} S.D\text{ = }\sqrt[]{\frac{\Sigma|x-\bar{x}|^2}{n}}=\sqrt[]{(462)/(6)}=\sqrt[]{77} \\ =8.775 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/t43p4c7ik4epselzgj8u827lprro0cdh3o.png)
Therefore, the standard deviation of the data set