From the given figure
There is a right triangle whose legs are x and 99, its hypotenuse is (x + 81)
By using the Pythagorean theorem
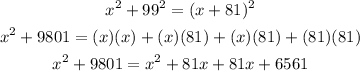
Add the like terms on the right side
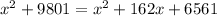
Subtract x^2 from both sides
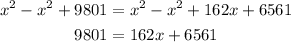
Subtract 6561 from both sides
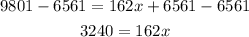
Divide both sides by 162
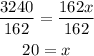
The value of x is 20