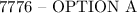Question

A fair sortition trial is carried out, and one of the candidates is assigned the number 32,041.If each digit can be chosen from 0-5, and if each of the possible sequences is assigned to a candidate, how many candidates are there?Group of answer choices7,77653,125625

Answer 1

Step 1:

In this question, we are given that:

A fair sortition trial is carried out, and one of the candidates is assigned the number 32,041.

If each digit can be chosen from 0-5, and if each of the possible sequences is assigned to a candidate, how many candidates are there?

Step 2:

We can use the fundamental counting theory to determine the number of possible ways in which a 5-digit can be assigned from zero to five.

In this case, the first to fifth digit can be assigned from zero to five.

Hence the sequence is :

`\begin{gathered} 6^5\text{ = 6 x 6 x 6 x 6 x 6 } \\ =\text{ 7776} \end{gathered}`

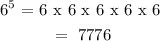
CONCLUSION:

The final answer is :

`7776\text{ -- OPTION A}`