Question

Given g(x) =✓x-4 and h(x)= 2x-8 what are the restrictions on the domain g*hx>or= ___

Answer 1

We have the following functions:

`\begin{gathered} g(x)=\sqrt[\square]{x-4} \\ h(x)=2x-8 \end{gathered}`

Step 1. Calculate the composition of the functions:

`g\circ h`

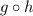
which is defined as follows:

`g\circ h=g(h(x))`

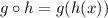
Thus, we need to substitute h(x) into the x in g(x):

`g\circ h=\sqrt[]{(2x-8)-4}`

Step 2. Simplify the expression:

`\begin{gathered} g\circ h=\sqrt[]{2x-8-4} \\ g\circ h=\sqrt[]{2x-12} \end{gathered}`

Step 3. Calculate the restrictions on the domain.

The domain of a function are the possible values for the variable x.

In this case, since we have a square root, we can only have possitive values inside of the square root.

Thus, we need 2x-12 to be equal or greater to 0:

`2x-12\ge0`

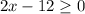
Step 4. Solve the inequality for x:

`\begin{gathered} 2x-12\ge0 \\ 2x\ge12 \\ x\ge(12)/(2) \\ x\ge6 \end{gathered}`

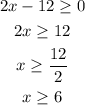
Answer:

x≥6