Question

A bag contains 9 red marbles, 10 white, 5 blue. If 6 are drawn at random, what is the probability of the questions below:1. That 3 blue are chosen. Round answer to five decimal places.2. That the same number of each colour are chosen. Round answer to five decimal places.3. That none will be red. Round answer to five decimals.4. That all six will be the same colour. Round answer to five decimal places. (Watch out for blue)

Answer 1

1) The experiment consists of picking 3 blue marbles and 3 of any other color.

Therefore, we can divide such an experiment into 6 dependent events whose probabilities are calculated below

`\begin{gathered} P_1(blue)=(5)/(9+10+5)=(5)/(24) \\ P_2(blue)=(4)/(9+10+4)=(4)/(23) \\ P_3(blue)=(3)/(9+10+3)=(3)/(22) \\ P_4(notblue)=(19)/(9+10+2)=(19)/(21) \\ P_5(notblue)=(18)/(20) \\ P_6(notblue)=(17)/(19) \end{gathered}`

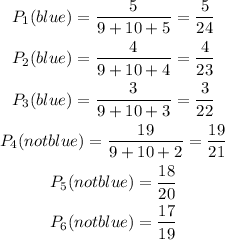
Therefore, the probability of the whole event is

`P=P_1*P_2*...*P_6=(51)/(14168)\approx0.0036`

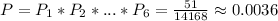
The answer to part 1) is 0.0036.

2) We need to pick 2 blue, 2 red, and 2 white marbles; therefore,

`\begin{gathered} P_1(blue)=(5)/(24),P_2(blue)=(4)/(23) \\ P_3(red)=(9)/(22),P_4(red)=(8)/(21) \\ P_5(white)=(10)/(20),P_6(white)=(9)/(19) \\ \Rightarrow P=P_1*...*P_6=(45)/(33649)\approx0.00134 \end{gathered}`

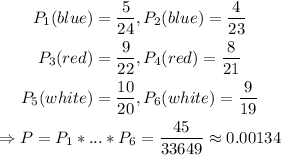
The answer to part 2) is 0.00134

3)

`\begin{gathered} P_1(nonred)=(15)/(24),P_2(nonred)=(14)/(23),...,P_6(nonred)=(10)/(19) \\ \Rightarrow P=(15!)/(9!)*(18!)/(24!)=(65)/(1748)\approx0.03719 \end{gathered}`

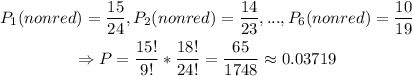
The answer to part 3) is 0.03719

4)

`\begin{gathered} P(allblue)=0 \\ P(allred)=(9!)/(3!)*(18!)/(24!)\approx0.00062 \\ P(allwhite)=(10!)/(4!)*(18!)/(24!)\approx0.00156 \end{gathered}`

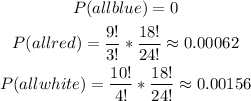
The probabilities of the three subevents in part 4 are shown above.