Question

Find the x-coordinate of point P that lies 1/3 along segment RS, closer to S, where R (-7, -2) and S (2, 4).

Answer 1

In a diagram,

On the other hand, the formula to obtain the distance between two points is

`\begin{gathered} A=(x_1,y_1),B=(x_2,y_2) \\ \Rightarrow d(A,B)=√((x_1-x_2)^2+(y_1-y_2)^2) \end{gathered}`

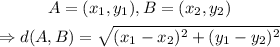
Therefore, in our case,

`\begin{gathered} 2*d(P,S)=d(P,R) \\ \end{gathered}`

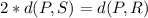
After setting R=(x,y), we get,

`\begin{gathered} \Rightarrow2*√((x-2)^2+(y-4)^2)=√((x+7)^2+(y+2)^2) \\ \Rightarrow4((x-2)^2+(y-4)^2)=(x+7)^2+(y+2)^2 \\ \Rightarrow(3x^2-30x-33)+(3y^2-36y+60)=0 \\ \Rightarrow(x^2-10x-11)+(y^2-12y+20)=0 \end{gathered}`

Furthermore, point P lies along RS, and the equation of such segment is

`\begin{gathered} equation\text{ RS} \\ y=(2)/(3)x+(8)/(3) \end{gathered}`

Substitute into the square root equation, so the expression only depends on x,

`\begin{gathered} \Rightarrow x^2-10x-11+(4)/(9)(x^2+8x+16)-8x-32+20=0 \\ \end{gathered}`

Solve for x, as shown below

`\begin{gathered} \Rightarrow(13)/(9)(x^2-10x-11)=0 \\ \Rightarrow x=-1,11 \end{gathered}`

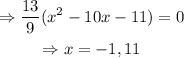
Notice that x=11 would imply that P is not between points R and S but to the 'right' of S.

Therefore, the only valid solution is x=-1.

Calculate the corresponding value of y for x=-1 using the equation of the line RS, as shown below

`\begin{gathered} x=-1 \\ \Rightarrow y=(2)/(3)(-1)+(8)/(3)=(6)/(3)=2 \\ \Rightarrow P=(-1,2) \end{gathered}`

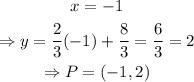
Therefore, the answer is P=(-1,2)