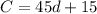Question

The cost C, to rent a car for d days is shown in the table

Answer 1

Step-by-step explanation

We are given the table below:

We are required to determine the equation that represents the function.

We know that the table follows a linear equation of the form:

`\begin{gathered} y=mx+b \\ \\ Now,C=md+b \\ where \\ C=cost \\ m=gradient\text{ }or\text{ }slope \\ d=days \\ b=y\text{ }intercept \end{gathered}`

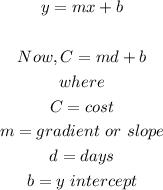
First, we can obtain the gradient of the function as:

`\begin{gathered} m=(\triangle y)/(\triangle x)=(\triangle C)/(\triangle d)=(C_2-C_1)/(d_2-d_1) \\ Using\text{ }the\text{ }ordered\text{ }pairs:(2,105)\text{ }and\text{ }(4,195) \\ where \\ d_1=2;C_1=105 \\ d_2=4;C_2=195 \\ \therefore m=(195-105)/(4-2)=(90)/(2)=45 \end{gathered}`

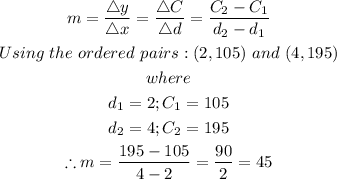
Therefore, the equation becomes:

`\begin{gathered} \begin{equation*} C=md+b \end{equation*} \\ C=45d+b \\ at\text{ the point }(2,105)\text{ i.e. }C=105;d=2 \\ 105=45(2)+b \\ 105=90+b \\ \therefore b=15 \\ \\ The\text{ }new\text{ }equation:C=45d+15 \end{gathered}`

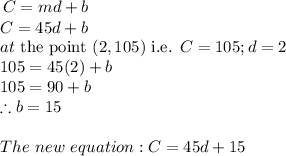
Hence, the equation that represents the function is:

`\begin{equation*} C=45d+15 \end{equation*}`