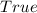Solution:
The coordinates (-6, 4) satisfy the equation:
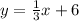
because
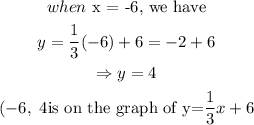
If (-6, 4) satisfies the equations of two lines, (-6, 4) is
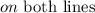
so that the lines will
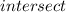
at (-6, 4).
This means that if two lines
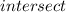
at (-6, 4), then (-6, 4) is the
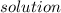
to the system of equations.
This means that if you substitute -6 for x and 4 for y in the equations, both equation will be