Answer:
• The slope of the line = -5/6
,
• The y-intercept of the line = 1/2
Explanation:
Given the equation of the line below:
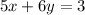
We are required to:
• Write the equation in ,slope-intercept form,.
,
• Find the slope and y-intercept of the line.
The slope-intercept form of the equation of a straight line is:

So, first, make y the subject of the given equation:
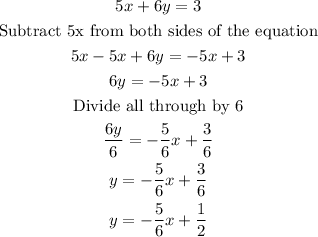
Next, compare with the form given above:
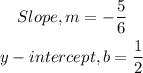
• The slope of the line = -5/6
,
• The y-intercept of the line = 1/2