5)
Before we see which model best fits the given data, let's plot the points into a graph, that's fundamental! Always plot the points for better visualization, only by plotting the points we can see what kind of model we will use, then, plotting these points we will get:
Here, we are using the y-axis as the life expectancy and the x-axis as the years after 1950. Only looking at the graph we can see that the points follows something like a line, therefore, we are looking for a linear model, like
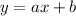
But what value of "a" and "b" best fits the points? We can find it, but it will take a lot of time and calculus, then, let's look at the graph and see which equation in the option is correct. We only have two options for linear models:
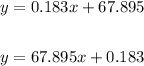
To see which one is correct we just look at the y-intercept (number without "x"), looking at our graph the y-intercept is something like 68.2, then, the correct answer is
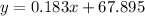
The final answer for 5) is the letter C.
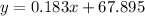
6)
Now we can use the equation of 5) to find it, let's find the value of x that we will input into the function, 1995 is 45 years after 1950, then, we will input x = 45.
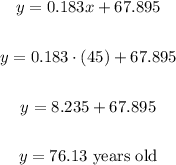
The predicted life expectancy for 1995 is 76.13 years old