The initial population given is
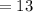
The percentage growth rate is

The Exponential function is given as
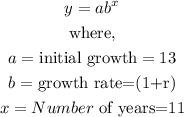
By substituting the values, we will have the exponential formula to be

By substituting the values of a and x in the formula above, we will have
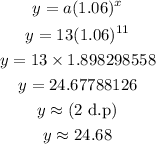
Therefore,
The final answer is = 24.68