Question

supposed that there are two types of tickets to a show :advance and same-day. advance tickets cost $25 and same-day tickets cost $40.for one performance, there were 60 tickets sold in all, and the total amount paid from them was $2,025. how many tickets of each type were soldnumber of advance tickets sold:number of same-day tickets sold:

Answer 1

• The number of advance tickets sold: 25

• The number of same-day tickets sold: ​35

Step-by-step explanation:

Let the number of advance tickets sold = a

Let the number of same-day tickets sold = s

Advance tickets = $25

Same-day tickets = $40.

`\begin{gathered} \text{For one performance, there were 60 tickets sold in all.} \\ a+s=60\ldots(1) \\ \text{The total amount paid from them was }2,025 \\ 25a+40s=2025\ldots(2) \end{gathered}`

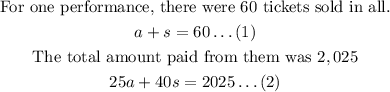
From equation (1):

`a=60-s`

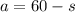
Substitute a=60-s into the second equation:

`\begin{gathered} 25(60-s)+40s=2025 \\ 1500-25s+40s=2025 \\ 15s=2025-1500 \\ 15s=525 \\ s=(525)/(15) \\ s=35 \end{gathered}`

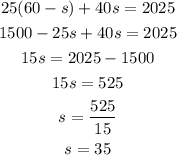
Recall: a=60-s

`\begin{gathered} a=60-35 \\ a=25 \end{gathered}`

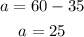
Therefore:

• The number of advance tickets sold: 25

,

• The number of same-day tickets sold: ​35