We have the cost function and the revenue function given as follows;

The profit is calculated by subtracting cost from sales, that is;
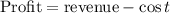
Therefore, we would now have;
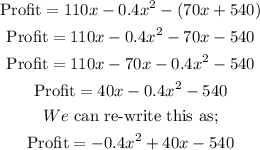
With the profit function we can now calculate the profit if we have the quantity produced (which is x). However, we have been given a weekly profit of $300, which means we can determine how many units are sold by inputing the profit into the profit function as follows;
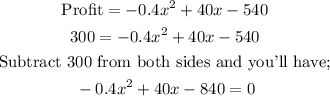
We can now solve this quadratic equation as follows;
![\begin{gathered} -0.4x^2+40x-840=0 \\ \text{Multiply all through by 10 to remove the decimal and we'll have;} \\ -4x^2+400-8400=0 \\ \text{Use the quadratic equation formula,} \\ x=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a} \\ \text{Where,} \\ a=-4,b=400,c=-8400 \\ x=\frac{-400\pm\sqrt[]{(400)^2-4(-4)(-8400)}}{2(-4)} \\ x=\frac{-400\pm\sqrt[]{160000-134400}}{-8} \\ x=\frac{-400\pm\sqrt[]{25600}}{-8} \\ x=(-400\pm160)/(-8) \\ x=(-400+160)/(-8),x=(-400-160)/(-8) \\ x=30,x=70 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/yoby9sp2umb77c5pawidgxomol49cpujqk.png)
From the results, we can see that to make a profit of $300 per week, the company needs to sell 70 or 30 units of the product.
ANSWER:
They need to sell 70 or 30 items