The given inequality is:
![-18\sqrt[]{2x-1}>-36](https://img.qammunity.org/2023/formulas/mathematics/college/k57cvc6s7a09gycjjmu7xerol0yjwt4f8q.png)
To find the solution start by dividing both sides by 18:
![\begin{gathered} \frac{-18\sqrt[]{2x-1}}{18}>-(36)/(18) \\ -\sqrt[]{2x-1}>-2 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/l5d3bxkc9ivao6q2q61g7meh46ogpxekd4.png)
Now, multiply both sides by -1:
![\begin{gathered} -\sqrt[]{2x-1}\cdot-1>-2\cdot-1 \\ As\text{ we are multiplying by a negative number, reverse the inequality symbol:} \\ \sqrt[]{2x-1}<2 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/mgt2k3kd2ismiospyihvhi444kt0dmwxhd.png)
Square both sides:
![\begin{gathered} \sqrt[]{2x-1}^2<2^2 \\ 2x-1<4 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/icl3xl0boy89o5jksk5emi0od85pn38b6h.png)
Add 1 to both sides:
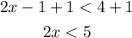
Divide both sides by 2:
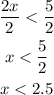
Also, the number inside the square root can't be negative, then:
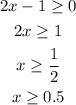
Then 0.5<=x<2.5, in the number line it will be:
The circle in 0.5 is closed and the circle in 2.5 is open.
![undefined]()