1 Answer

FiveTools · Answer 1 · 2023-12-19T13:31:01+0000

Answer:

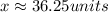
$x\approx36.25units$

The given triangle is an isosceles triangle with a height of 33 units and a base of 30 units.

To get the value of x, we will use the Pythagoras theorem on one of the right angles formed by the triangle as shown:

According to the theorem;

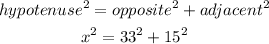
$\begin{gathered} hypotenuse^2=opposite^2+adjacent^2 \\ x^2=33^2+15^2 \end{gathered}$

Simplify the equation for the value of "x"

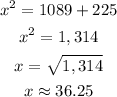
$\begin{gathered} x^2=1089+225 \\ x^2=1,314 \\ x=√(1,314) \\ x\approx36.25 \\ \end{gathered}$

Hence the value of x from the figure is approximately 36.25 units