Given the definite integral to find the total area between the graph of f(x)
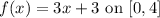
We first want to set up a Riemann sum. Based on the limits of integration, we have a = 0 , b = 4
![Fori=0,1,2,\ldots,n,letP=\mleft\{\xi\mright\}bearegularpartitionof\mleft[0,4\mright].Then](https://img.qammunity.org/2023/formulas/mathematics/college/e8k7p354aywa9y5w24y93mqj568http84k.png)
Since we are using a right-endpoint approximation to generate Riemann sums, for each i, we need to calculate the function value at the right endpoint of the interval [xi−1,xi]. The right endpoint of the interval is xi, and since P is a regular partition,

Thus, the function value at the right endpoint of the interval is
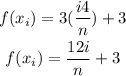
Then the Riemann sum takes the form
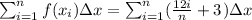
Therefore,
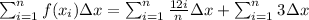
Hence,

Thus,
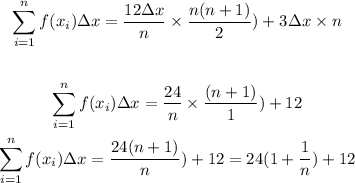
Hence,
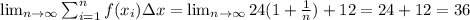
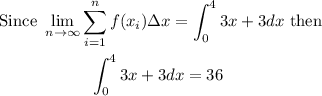
Therefore the definite integral for the function is 36