The conditional probability is given by:
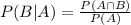
Let A be the event "the student is male" and B the event "First class is humanities".
The probability of A is:
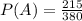
The probability of event A and B is:

Therefore the conditional probability is:

Therefore the probability we are looking for is 10/43