The area of a circle is given by the next formula:
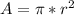
___________
For the given expression of area:
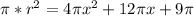
Use the equation above to solve r (radius):
1. Divide both sides of the equation into π
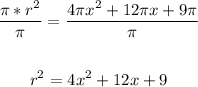
2. Factor the expression on the right using the notable product perfect square binomial:
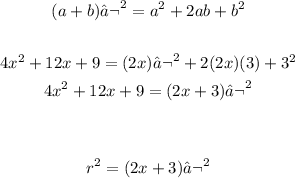
3. Find square root of both sides of the equation:
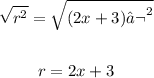
Then, the radius is given by the expression 2x+3.
______________________________
To find the least possible integer value of x: As r is the radius of a circle, it cannot be a negative amount or 0, then r needs to be greather than 0:
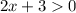
Solve the ineqaulity above:
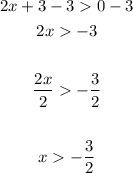
x needs to be greater than -3/2 (-1.5).
Then, the least possible integer value of x is -1