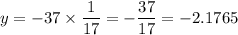Answer:
2.1765
Explanation:
We have the following relationship
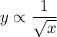
We can represent this inverse proportional relationship as
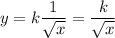
k is known as the constant of proportionality
Therefore
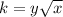
Given y = -37 when x = 289
k = -37 x √289
= -37 x 17
= - 629
We are asked t find y when x = 83521
With k = - 629 and x = 83521
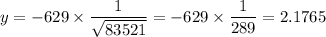
We can check if this is correct by noting that according to the rule of proportions:
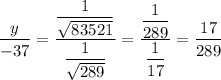
So