Question

A rock is dropped Into a calm pond, causing ripples to expand in the form of circles. The radios of the putter ripple is increasing at a rate of 2 feet per second. When the radios is 6 feet what is the rate of change of the total area of the circle?

Answer 1

First, let's define a function fo the radius in term of the time, in secons, since the rock hit the pond:

`r(t)=2t`

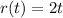
Now, we know that the area of the circle, in terms of the radius is:

`A(r)=\pi r^2`

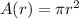
But since we know that the radius is a function of time,

`\begin{gathered} A(r(t))=\pi(2t)^2 \\ \\ \Rightarrow(A\circ r)(t)=4\pi t^2 \end{gathered}`

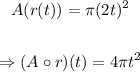
This way, we'll have that:

`(A\circ t)^(\prime)(t)=8\pi t`

Now, we find the time at which the radius was 6 feet:

`\begin{gathered} 6=2t\rightarrow(6)/(2)=t \\ \Rightarrow t=3 \end{gathered}`

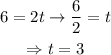
Now,

`\begin{gathered} (A\circ t)^(\prime)(3)=8\pi(3) \\ \\ \rightarrow(A\circ t)^(\prime)(3)=75.40 \end{gathered}`

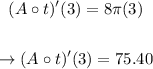
Therefore, we can conclude that the rate of change of the total area of the circle when the radius is 6 feet is 75.40 square feet per second.