Two parallel lines have the same slope. Given the equation of one of the lines, you can determine the slope of the other line:
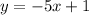
The slope of the line is the coefficient of the x-term, in this case, that coefficient is -5. Then the slope of both parallel lines is m= -5.
The line you have to find must cross through the point (9,-42). Using the point-slope form you can determine the equation of the parallel line:

Where
m is the slope of the line
(x₁,y₁) are the coordinates of one point of the line:
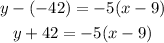
To write the equation in slope-intercept form, the first step is to distribute the multiplication on the parentheses term:
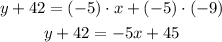
Subtract 42 to both sides of the expression to pass the term to the right side of the equal sign:
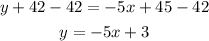
The equation of the line is y= -5x + 3