We have the equation:
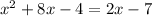
We have to compare it to the equation:
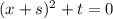
We start by rearranging the first equation:
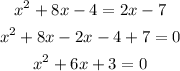
We then add a term to find the square in order to factorize it as the second equation:
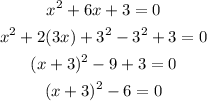
Then, comparing to the second equation, s = 3 and t = -6.
Answer: the value of t for this quadratic equation is t = -6.