Question

ERROR ANALYSIS In Exercise 30, describe and correct the error in finding the inverse of the functionf(x)=1/7x^2, x>=0y=1/7x^2x=1/7y^27x=y^2+-√7x=y

Answer 1

Given the function

`\begin{gathered} f(x)=(1)/(7)x^2 \\ x\ge0 \end{gathered}`

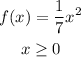
To find the inverse, we must recall that the domain of the function becomes the range of the inverse function and vice-versa.

We are already given the domain of f, all the real numbers equal or greater than zero.

The domain of the function is exactly the same because x squared is always positive or zero, thus the domain and range of the inverse should be x≥0.

Once we find the inverse function, we'll use this concept.

Step 1: Substitute f(x) for y:

`y=(1)/(7)x^2`

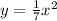
Step 2: Swap the variables:

`x=(1)/(7)y^2`

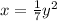
Step 3: Solve for y:

`y=\pm\sqrt[]{7x}`

But as said above, the range of this function cannot include the negative numbers, thus the inverse function is:

`f^(-1)(x)=\sqrt[]{7x}`