We are given the following two points

We are asked to find the equation of the line that passes through these points.
Recall that the equation of the line in slope-intercept form is given by

Where m is the slope and b is the y-intercept.
The slope of the line is given by
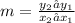
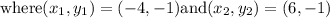
Let us substitute the given values into the slope formula
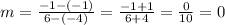
So, the slope of the equation is 0
The equation of the line becomes
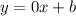
Now let us find the y-intercept (b)
Choose any one point from the given two points
Let choose (-4, -1) and substitute it into the above equation
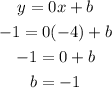
Therefore, the equation of the line in slope-intercept form is
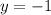
Note that this equation has 0 slope that is why mx part becomes 0