We will solve this in steps to understand better! :)
Solution :
We have
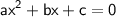 here a ≠ 0
here a ≠ 0
Step 1 : Subtract 'c' from both sides of this equation
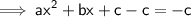
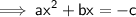
Step 2 : Dividing both side by coefficient of x² i.e 'a' [why? because we want the coefficient of x² as 1]
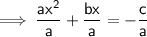
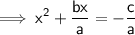
Step 3 : Adding
 i.e,
i.e,
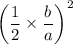
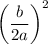 to both sides
to both sides
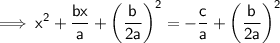
Step 4 : From the left side of equation an identity is formed i.e (a + b)² which is equal to a² + 2ab + b²
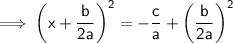
Note : If we expand
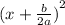 it will again form
it will again form
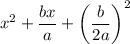
Step 5 : Solving!
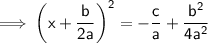
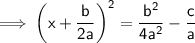
Here, [On right side of equation for LCM]
4a² = 4×a×a
a = a
Hence LCM = 4a²
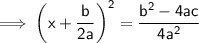
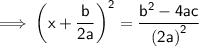
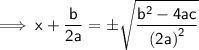
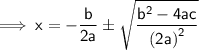
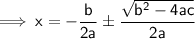
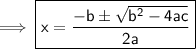
Our quadratic formula is formed!
Therefore,
The roots of general quadratic equation are
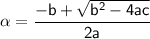
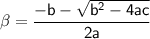
Sum of roots
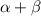
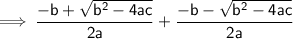
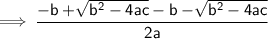
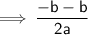
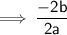
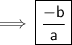
So, the sum of roots = -b/a
Now,
Product of roots =
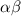
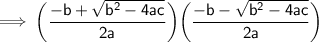
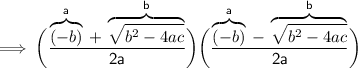
Using (a + b) (a - b) = a² - b²
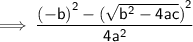
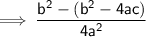
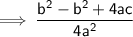
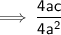
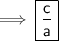
So, Product of roots = c/a
We are done with our solution! :D
Note :
Move from left to right to see the full answer.