Question

The equation V = 16300 (0.94)^t represents the value (in dollars) of a car t years after its purchase. Use this equation to complete the statements below.

Answer 1

Given:

`V=16300(0.94)^t`

The value of a car after t - years will depreciate.

Hence, the equation given represents the value after depreciation over t-years.

To get the rate, we compare the equation with the depreciation formula.

`\begin{gathered} A=P(1-r)^t \\ \text{where;} \\ P\text{ is the original value} \\ r\text{ is the rate} \\ t\text{ is the time } \end{gathered}`

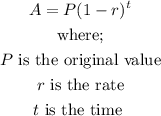
Hence,

`\begin{gathered} V=16300(0.94)^t \\ A=P(1-r)^t \\ \\ \text{Comparing both equations,} \\ P=16300 \\ 1-r=0.94 \\ 1-0.94=r \\ r=0.06 \\ To\text{ percentage,} \\ r=0.06*100=6\text{ \%} \\ \\ \text{Hence, } \\ P\text{ is the purchase price} \\ r\text{ is the rate} \end{gathered}`

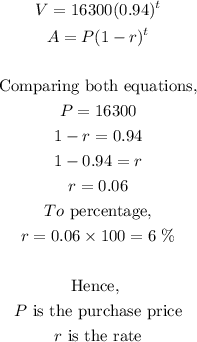
Therefore, the value of this car is decreasing at a rate of 6%. The purchase price of the car was $16,300.