Question

Carol drops a stone into a mine shaft 272 meters deep. The average temperature of the air inside the shaft is 4.5 degrees Celsius. How soon after she drops the stone does she hear it hit the bottom of the shaft? Include units in your answer.

Answer 1

The stone takes a time t₁ to reach the bottom of the mine shaft. Then, the sound travels all the way up during a time t₂.

Use the equations of free fall motion to find the time that it takes for the stone to reach the bottom of the mine shaft. Next, use the relation between the speed of sound and temperature to find the speed of sound at 4.5ºC, use that speed to find the time that it takes for the sound to reach the surface. Finally, add both times to find the total time that it takes for Carol to hear the hit.

Step 1: Stone falling down.

The time that it takes for any object under the influence of the gravitational field of the Earth at its surface to fall a distance h is given by the formula:

`t=\sqrt[]{(2h)/(g)}`

Where g is the acceleration of gravity:

`g=9.81(m)/(s^2)`

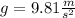
Replace the value of g and h=272m to find the time that it takes for the stone to hit the bottom of the shaft:

`t_1=\sqrt[]{(2(272m))/(9.81(m)/(s^2))}=7.446718657\ldots s`

Step 2: Speed of sound

The speed of sound at a temperature of 20ºC is:

`v_(20ºC)=343(m)/(s)`

Additionally, the speed of sound is proportional to the square root of the absolute temperature of the air:

`v=k\cdot\sqrt[]{T_{\text{abs}}}`

Which means that for two different values of temperature, we have that:

`\frac{v_1}{\sqrt[]{T_1}}=\frac{v_2}{\sqrt[]{T_2}}`

Let v₁ represent the speed of sound at a temperature of 4.5ºC and v₂ the speed of sound at a temperature of 20ºC. Add 273.15 to each temperature in celsius to write them using the absolute scale of temperature (Kelvin):

`\begin{gathered} 4.5ºC=4.5K+273.15KK=277.65K \\ 20ºC=20K+273.15K=293.15K \end{gathered}`

Isolate v₁ from the equation. Then, replace the values of the known temperatures and speeds to find the speed of sound at 4.5ºC:

`\begin{gathered} v_1=\frac{\sqrt[]{T_1}}{\sqrt[]{T_2}}* v_2 \\ =\frac{\sqrt[]{277.65K}}{\sqrt[]{293.15K}}*343(m)/(s) \\ =333.8089754\ldots(m)/(s) \end{gathered}`

Since the sound wave travels a distance of 272 meters at a constant speed of 333.81 meters per second, the time it takes for the sound of the stone to reach the top of the shaft is:

`t_2=(h)/(v)=(272m)/(333.8089754\ldots(m)/(s))=0.8148372874\ldots s_{}`

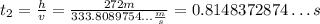
Step 3: Time

Add the time that it takes for the stone to hit the bottom of the shaft and the time it takes for the sound wave to reach the top of the shaft to find the total time that it takes for Carol to hear the stone hitting the bottom after she drops it:

`t=7.4467\ldots s+0.8148\ldots s=8.261\ldots s`

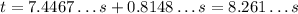
Therefore, Carol hears the stone hitting the bottom of the shaft approximately 8.3 seconds after she drops it.