Question

wrote the equation of a line that is perpendicular to the given line and that passes through the given point.y-5=-3(x-1); (1, 5)

Answer 1

The two lines are said to be perpendicular if the product of thier slope is equal to the -1

The general equation of line:

`y-y_1=m(x-x_1)`

where, m is the slope of the line

The given expression : y - 5 = -3(x -1 )

Simplify the expression:

`\begin{gathered} y-5=-3(x-1) \\ On\text{ comparing with the general form of line } \\ we\text{ get: m =(-3)} \end{gathered}`

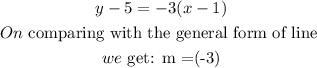
Slope of the given line is m = (-3)

Let the slope of the second line is n

From the condition of the perpendicular lines

`\begin{gathered} \text{Slope of line1}* Slope\text{ of line 2= -1} \\ m* n=-1 \\ (-3)* n=-1 \\ n=(1)/(3) \end{gathered}`

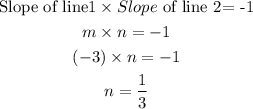
Slope of the second line which is perpendicular to the given line is 1/3

Use the general form of equation of line to get the expression pf line2:

The passing points : (1,5)

`\begin{gathered} y-y_1=m(x-x_1) \\ y-5=(1)/(3)(x-1) \end{gathered}`

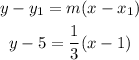
The equation of line which is perpendicular to the line y-5=-3(x-1) is y - 5 = 1/3 (x - 1 )

Answer : y - 5 = 1/3 (x - 1 )