We are given a random variable with a normal distribution and we are asked the following:
Part A.

We need to determine the z-score for this value. To do that we will use the following formula:

Now we substitute the values:
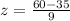
Solving the operations:
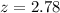
Therefore, we have:
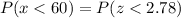
From the table of probabilities for normal distribution we get:
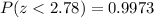
Therefore, the probability that x is less than 60 is 0.9973
Part B. We are asked the following:
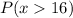
We need to determine the z-score for this value. We use the same formula as in part A:

Solving the operations we get:
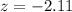
Therefore, we have:
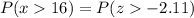
Since the table will give us only the values that are less than -2.11 we need to use the following relationship:

From the table we get:
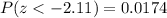
Substituting we get:
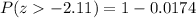
Solving the operations we get:
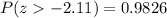
Therefore, the probability that x is greater than 16 is 0.8257
Part C. We are asked the following:
![P(16To determine that, we will use the following formula:<p></p>[tex]P(16We have already determined the formula for these probabilities in parts A and B. Therefore, we substitute and we get:<p></p>[tex]P(16Solving the operations we get:<p></p>[tex]P(16Therefore, the probability that x is between 16 and 60 is 0.9799.<p>Part C. We are asked the following:</p><p></p>[tex]P(x>60)]()
We use the same relationship as is part B:
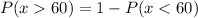
We already determine the probability that x is less than 60 in part A, therefore, we substitute and we get:
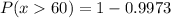
Solving the operations we get:
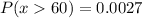
Therefore, the probability that x is more than 60 is 0.027.