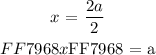Question

Will someone help me with all of these, I have the answers but I’m trying check them.This is a practice assignment btw.

Answer 1

We will look at the process of solving literal equations for a particular variable ( x ).

A literal equation is usually categorized by a myraid of constants that are crucial to the process which is being modeled. We solve such equation in terms of a controlling variable ( that we can choose to alter our process ).

For the following literal equations ( x ) will be the subject of variability.

`3\cdot(bx\text{ - 2ab ) = }b\cdot(x-7a)\text{ + 3ab}`

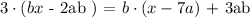
Whenever we have algebraic expressions we always refer to the rule of ( PEMDAS ).

Step 1: Solve the Parenthesis

We will solve for all the parenthesis in the equation given and write down the result:

`3bx\text{ - 6ab = bx - 7ab + 3ab }`

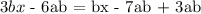
Step 2: Highlight and combine the like terms

All like terms are classified on the basis of their constants ( a and b ) and variable ( x ) attached. We will highlight all the like terms and take simplify them on either side of the " = " sign:

`\begin{gathered} 3bx\text{ }\text{\textcolor{#FF7968}{- 6ab}}\text{ = bx }\text{\textcolor{#FF7968}{-7ab}}\text{ }\text{\textcolor{#FF7968}{+ 3ab}} \\ 3bx\text{ - bx = 2ab} \end{gathered}`

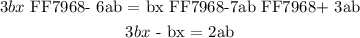
We combined three like terms ( -6ab , -7ab , and 3ab ).

Step 3: Factorize and simplify the equation

Now we will look for any constant that is present in all the terms throughout the equation. We see that constant ( b ) is common in all the terms. Hence, we will factor ( b ) out and cancel it out from each side of the " = " sign as follows:

`\begin{gathered} b\cdot(3x\text{ - x ) = b}\cdot(2a) \\ \textcolor{#FF7968}{2x}\text{\textcolor{#FF7968}{ = 2a}} \end{gathered}`

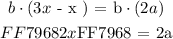
Step 4: Solve for the variable ( x )

We are left with a simple expression that relates the constant ( a ) and variable ( x ). We can go ahead and solve for the above:

`\begin{gathered} x\text{ = }(2a)/(2) \\ \textcolor{#FF7968}{x}\text{\textcolor{#FF7968}{ = a}} \end{gathered}`