In an isosceles trapezoid, the base angles are congruent, so the angle ∠1 is congruent to the angle 88°, so we have ∠1 = 88°.
Also, In any trapezoid, the consecutive angles in each base are supplementary, so we have:
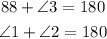
Solving these equations for ∠2 and ∠3, we have:
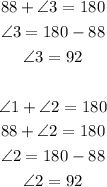
So we have that ∠2 = 92° and ∠3 = 92°.